Energy-Preserving Operator Inference

Abstract:

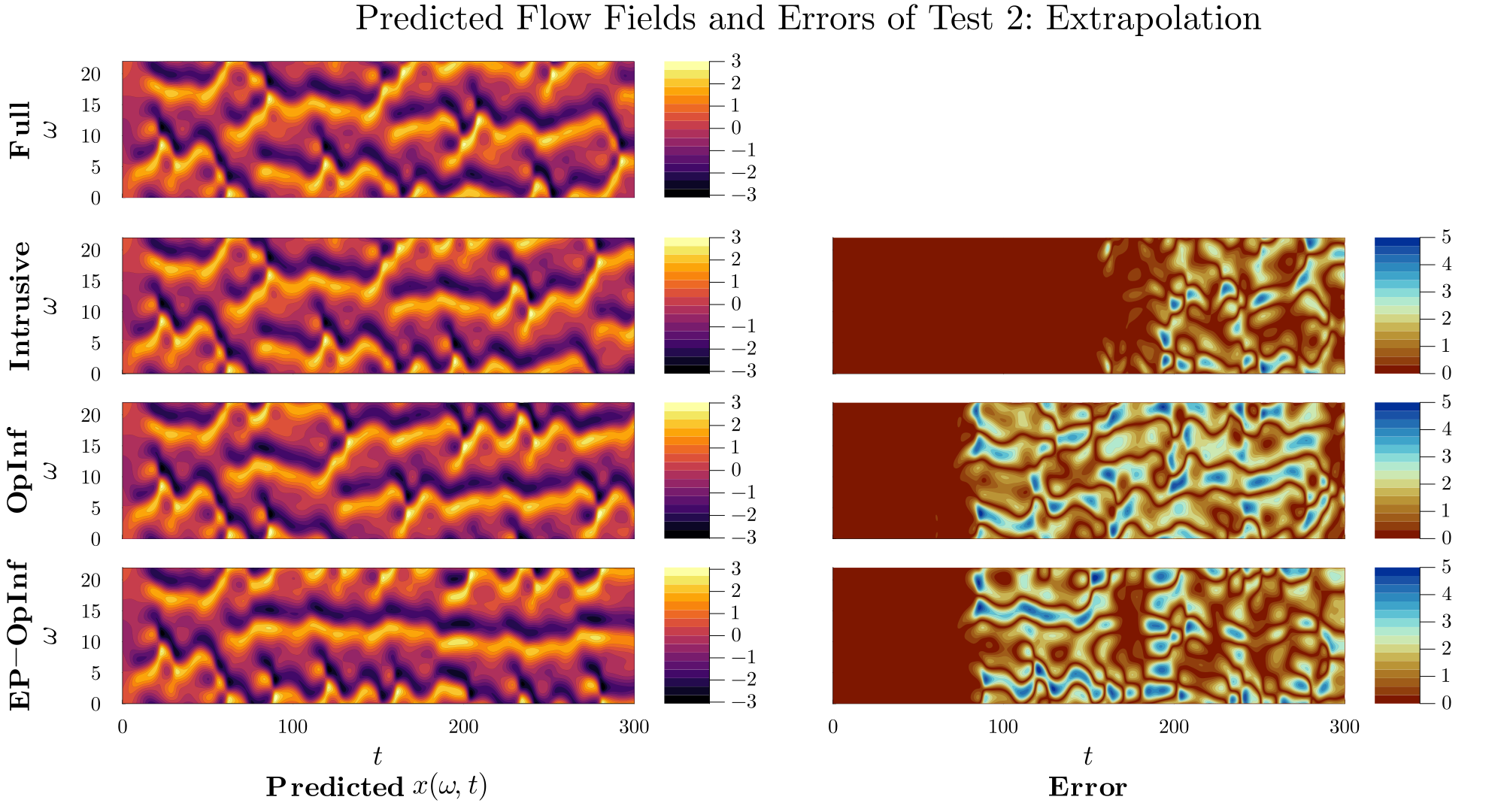
Many-query computations, in which a computational model for an engineering system must be evaluated many times, are crucial in design and control. For systems governed by partial differential equations (PDEs), typical high-fidelity numerical models are high-dimensional and too computationally expensive for the many-query setting. Thus, efficient surrogate models are required to enable low-cost computations in design and control. This work presents a physics-preserving reduced model learning approach that targets PDEs whose quadratic operators preserve energy, such as those arising in governing equations in many fluids problems. The approach is based on the Operator Inference method, which fits reduced model operators to state snapshot and time derivative data in a least-squares sense. However, Operator Inference does not generally learn a reduced quadratic operator with the energy-preserving property of the original PDE. Thus, we propose a new energy-preserving Operator Inference (EP-OpInf) approach, which imposes this structure on the learned reduced model via constrained optimization. Numerical results using the viscous Burgers’ and Kuramoto-Sivashinksy equation (KSE) demonstrate that EP-OpInf learns efficient and accurate reduced models that retain this energy-preserving structure.